ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
1. Введение
В этой работе Вы познакомитесь с численными методами решения систем линейных алгебраических уравнений. Все рассматриваемые методы ориентированы на решение систем уравнений большой размерности. Подобные системы возникают на практике, например, при интегрировании уравнений в частных производных эллиптического типа.
Везде далее будем рассматривать линейное
пространство 
Будем
также считать, что x, 
k = 0, 1, 2, …, являются элементами пространства Кроме того, под А будем
понимать тот или иной линейный оператор, действующий из 
в
Запишем систему линейный уравнений в следующем виде:
(4.1)
Предполагается, что определитель матрицы A отличен от нуля, так что решение существует и оно единственно.
Численные методы решения системы (4.1) делятся на две группы: прямые и итерационные.
В прямых методах точное решение находится за конечное число арифметических действий. Примерами прямых методов являются метод Гаусса и метод сопряженных градиентов.
Каждый
итерационный метод состоит в том, что при решении системы (4.1) указывается
рекуррентное соотношение, которое по заданному произвольно «нулевому»
приближению 
решения
x позволяет вычислить первое, второе, …, p-е
приближение 
(p = 1, 2, 3, …) решения x.
Иногда необходимо решить уравнение (4.1), в котором A — линейный оператор, не заданный явно в виде матрицы. В этом случае прямые методы в отличие от итерационных, могут быть неприменимы.
В данной работе для итерационных методов дается наглядная иллюстрация изменения нормы разности двух последовательных приближений. Эффективность различных методов (в том числе прямых) можно сравнить по затратам машинного времени (необходимая информация выводится на экран), которое необходимо для достижения заданной точности, т. е. до тех пор, пока не будет выполнена оценка
Задача отыскания точного решения уравнения (4.1) не диктуется, как правило, запросами приложений. Обычно допустимо использование приближенного решения, известного с достаточной точностью. Поэтому во многих случаях для вычисления решения уравнения (4.1) точным методам целесообразно предпочесть тот или иной итерационный метод.
Итерационный
процесс должен быть построен так, чтобы последовательность приближений 
стремилась к решению x уравнения (4.1). Тогда для любого e > 0 существует номер 
такой, что Задавая e > 0 достаточно малым,
можно воспользоваться n-м приближением x.
Представлены следующие девять методов:
1) Гаусса;
2) сопряженных градиентов;
3) простых итераций;
4) с оптимальным параметром;
5) с оптимальным набором параметров;
6) Зейделя;
7) трехслойный метод Чебышева;
8) минимальных невязок;
9) скорейшего спуска.
2. Теоретическая справка
2.1. Обусловленность систем линейных уравнений
Две на первый взгляд похожие системы линейных уравнений могут обладать различной чувствительностью к погрешностям задания входных данных. Это свойство связано с понятием обусловленности системы уравнений.
Числом
обусловленности линейного оператора A, действующего в нормированном
пространстве 
а
также числом обусловленности системы линейных уравнений Ax = f назовем величину
Таким образом, появляется связь числа обусловленности с выбором нормы.
Предположим,
что матрица и правая часть системы заданы неточно. При этом погрешность матрицы
составляет dA, а правой части — df. Можно показать, что для
погрешности dx
имеет место следующая оценка (
):
В частности, если dA = 0, то
При этом решение уравнения Ax = f не при всех f одинаково чувствительно к возмущению df правой части.
Свойства числа обусловленности линейного оператора:
1. 
причем максимум и минимум берутся
для всех таких x, что 
Как следствие,
2. 
3 
где 
и 
— соответственно минимальное и максимальное
по модулю собственные значения матрицы A. Равенство достигается для
самосопряженных матриц в случае использования евклидовой нормы в пространстве 
4. 
Матрицы с большим числом обусловленности (ориентировочно
) называются плохо
обусловленными матрицами. При численном решении систем с плохо обусловленными
матрицами возможно сильное накопление погрешностей, что следует из оценки для
погрешности dx. Исследуем вопрос о погрешности решения, вызванной ошибками округления
в ЭВМ при вычислении правой части. Пусть t — двоичная разрядность чисел
в ЭВМ. Каждая компонента 
вектора правой части округляется с относительной
погрешностью 
Следовательно,
Таким образом, погрешность решения, вызванная погрешностями округления, может быть недопустимо большой в случае плохо обусловленных систем.
2.2. Метод Гаусса
Метод Гаусса является прямым методом. Запишем систему линейных уравнений в виде:
................................................................. (4.1а)
Пусть 
Выполнения этого условия всегда
можно добиться перенумерацией компонент вектора x, либо перестановками
уравнений. Тогда запишем первое из уравнений (4.1а) в виде
(4.2)
Вычтем это уравнение, умноженное
на соответствующий коэффициент 
из i-го уравнения системы (4.1а),
где i > 1.
Тогда эти уравнения преобразуются к виду
................................................................. (4.3)
Первая
компонента вектора x не входит в подсистему (4.3).
Выполним с (4.3) те же операции, что и ранее с системой уравнений (4.1а). В
результате получим новую подсистему уравнений, в которую уже не будут входить 
и 
Она дополняется уравнением (4.2)
и первым уравнением системы (4.3), не содержащим 
Уже после m – 3 подобных
циклов мы получаем подсистему из одного уравнения с одним неизвестным. При этом
матрица системы будет иметь треугольный вид. Совокупность операций по
приведению системы уравнений к такому виду называется прямым ходом метода
Гаусса. Решение системы с треугольной матрицей не вызывает затруднений.
Совокупность операций по нахождению решения системы с треугольной матрицей
называется обратным ходом метода Гаусса.
Общее число
арифметических операций при решении системы (4.1а) методом Гаусса составляет 
В приложениях матрица A часто имеет трехдиагональный вид, т. е. ненулевые элементы матрицы располагаются на главной диагонали и двух близлежащих к ней. Применение метода Гаусса к такой системе уравнений называется методом прогонки.
Метод Гаусса может оказаться неустойчивым по отношению к росту вычислительной погрешности.
Теорема 1. Для устойчивости метода Гаусса достаточно диагонального преобладания, т. е. выполнения неравенств
d > 0, i = 1, 2, …, m.
Вычислительную погрешность метода Гаусса можно
уменьшить, если применить модификацию метода, называемую методом Гаусса с
выделением главного элемента. Суть этой модификации заключается в
следующем. Нумерация компонент вектора x и уравнений выбирается так,
чтобы 
являлся
максимальным по модулю элементом матрицы A. Затем, после исключения 
перенумерацией строк и
столбцов добиваются того, чтобы 
в (4.3) являлся максимальным по модулю
элементом матрицы системы (4.3). Подобная процедура продолжается и далее.
При расчете на реальной ЭВМ с заданным числом разрядов, наряду с влиянием неточного задания входных данных на каждой арифметической операции, вносятся ошибки округления. Влияние последних на результат зависит не только от разрядности машины, но и от числа обусловленности матрицы системы, а также от выбранного алгоритма. Существуют алгоритмы, учитывающие влияние ошибок округления и позволяющие получить результат с гарантированной точностью, если система не обусловлена настолько плохо, что при расчете с заданной разрядностью эта точность не может быть гарантирована.
2.3. Метод сопряженных градиентов
Пусть матрица A системы (4.1) самосопряженная и положительно-определенная:
Запись A > 0
означает, что для любого 
такого что 
выполнено
где a > 0.
Метод
сопряженных градиентов может применяться и как прямой, и как итерационный.
Итерационный метод не уступает по скорости сходимости методу Чебышева, который
будет рассмотрен ниже, но выгодно отличается от последнего тем, что не требует
знания границ спектра. В то же время, метод сопряженных градиентов уступает
методу Чебышева, поскольку является неустойчивым для плохо обусловленных матриц
высокой размерности.*
В точной арифметике этот метод дает точное решение не позднее p
итераций, где p — число различных собственных значений. Наиболее
благоприятная ситуация для применения метода сопряженных градиентов имеет
место, если границы спектра неизвестны, а порядок m системы много больше
числа итераций k, при котором погрешность на k-й итерации 
удовлетворяет поставленному требованию
точности.
Метод сопряженных градиентов можно рассматривать как модифицированный вариант метода наискорейшего спуска (см. ниже).
Рассмотрим квадратичную форму
Поскольку
где 
— решение системы (4.1), и 
то решение задачи (4.1)
эквивалентно минимизации 
Для градиента 
справедливо выражение
В этом направлении функционал обладает наибольшей
мгновенной скоростью изменения.
Для метода сопряженных градиентов следующее приближение к решению выбирается по формуле
где 
— «вектор направления». Параметр 
выбирается таким
образом, чтобы вектор был
A-сопряженным с вектором 
а значение вычисляется из условия минимума 
Вычислительный алгоритм состоит в следующем.
Зададим произвольный вектор 
и построим последовательность
(4.4)
где
k = 0, 1, 2, …, (4.5)
k = 1, 2, …
Оказывается,
что существует номер 
такой, что член 
последовательности (4.4)
совпадает с точным решением x:
(4.6)
Элементы
последовательности 
…, 
являются уточняющимися с ростом
номера k приближениями к решению; при заданном малом e, e > 0,
погрешность 
приближения
при некоторых
условиях может стать меньше e даже при
значениях k << m.
Можно
показать, что «вектор направления» с точностью до скалярного множителя
представляет собой проекцию градиента 
на пространство, натянутое на векторы 
…, 
а векторы 
…, 
являются взаимно A-сопряженными.
Отсюда следует название метода — «сопряженных градиентов».
В настоящее время метод сопряженных градиентов при «умеренном» числе обусловленности и больших m используется обычно именно как метод последовательных приближений.
Попытка
вычисления точного решения при большом числе обусловленности и большом m
с помощью последовательности (4.4) и с учетом равенства (4.6) может
натолкнуться на препятствие, состоящее в возможной потере вычислительной
устойчивости при нахождении членов 
последовательности (4.4).
Заметим, что для применения метода не обязательно,
чтобы система была задана в каноническом виде 
i = 1, 2, …, m, или приведена к такому виду. К тому же нет необходимости
хранить матрицу A, которая имела бы 
элементов, в то время как векторы 
и 
записанные в координатной форме,
задаются лишь m числами каждый.
2.4. Метод простых итераций
Заметим, что систему линейных уравнений
(4.7)
можно преобразовать к виду
(4.8)
причем новое уравнение (4.8) равносильно исходному при любом значении t. Вообще, (4.7) многими способами можно заменить равносильной системой вида
(4.9)
частным случаем которой является (4.8).
Итерационная
схема при заданном произвольно имеет следующий вид
p = 0, 1, … (4.10)
при заданном произвольно .
Ниже приведены условия, при которых последовательность (4.10) сходится к решению системы (4.7).
Рассмотрим частный случай итерационной формулы (4.10):
p = 0, 1, … (4.11)
Для вычисления по этой формуле
достаточно уметь по заданному 
находить элемент 
получающийся в
результате действия оператора A.
Таким образом,
итерационный процесс вычисления решения системы Ax = f, в отличие от
метода Гаусса, можно реализовать и в случае операторной формы задания системы
линейных уравнений, не выделяя какой-либо базис в и не приводя к каноническому виду
i = 1, 2, …, m. (4.12)
Для некоторых
классов систем линейных уравнений число арифметических действий, необходимых
для получения решения с разумной точностью итерационными методами много меньше,
чем 
Теорема 2.
(Достаточное условие сходимости). Пусть в 
фиксирована некоторая норма, причем
соответствующая норма оператора B
равносильной системы (4.9) оказалась меньше единицы:
(4.13)
Тогда
система (4.7) имеет одно и только одно решение x; при
любом из
последовательность
(4.10) сходится к решению x, причем погрешность p-го
приближения (или p-й итерации)
удовлетворяет оценке
(4.14)
Тем самым,
норма погрешности 
стремится
к нулю с ростом p не медленнее геометрической прогрессии 
Замечание. Условие (4.13) может нарушаться
при каком-нибудь другом выборе нормы 
Однако сходимость сохранится, причем
оценка (4.14) заменится оценкой
где C — некоторая постоянная, зависящая от новой нормы, а знаменатель прогрессии q — прежний.
Теорема 3. (Необходимое и достаточное условие сходимости). Для того, чтобы итерационный процесс (4.10) сходился при любом начальном приближении, необходимо и достаточно, чтобы все собственные значения B лежали внутри единичного круга.
Замечание.
В условиях теоремы при проведении вычислений в реальной арифметике (с
ограниченным числом значащих цифр) метод простых итераций может оказаться
неустойчивым к росту ошибок округления. Например, если спектральный радиус матрицы
B меньше единицы, а 
(См. пример из задания.)
2.5. Метод Зейделя и метод релаксации
Итерационная схема имеет вид
Здесь B — треугольная матрица, содержащая выше главной диагонали нули, а на главной диагонали и ниже ее — элементы матрицы A:
Теорема 4. (Достаточное условие сходимости). Пусть A — вещественная симметричная положительно определенная матрица. Тогда метод сходится при любом начальном приближении.
Если для отыскания следующего приближения используется итерационная схема вида
где D
— диагональная матрица с элементами 
на главной диагонали, то такой метод
называется методом релаксации.
В случае 
метод называется методом
верхней релаксации. Обычно полагают 
Очевидно, что в случае 
метод релаксации совпадает с
методом Зейделя.
2.6. Метод простых итераций с оптимальным параметром
Пусть
матрица А в (4.1) самосопряженная и положительно-определенная: 
Собственные числа l в этом случае действительные положительные числа.
Пусть известны
наименьшее и
наибольшее собственные
значения A. Зададим произвольное приближение и рассмотрим последовательность
простых итераций:
p = 0, 1, …
Справедлива следующая теорема.
Теорема 5. 1) Если t достаточно мало, а именно, удовлетворяет неравенствам
(4.15)
то последовательность сходится к решению
x системы уравнений Ax = f, причем
гарантировано убывание нормы погрешности 
при возрастании p в
соответствии с оценкой
p = 0, 1, … (4.16)
Здесь q < 1 и дается выражением:
(4.17)
т. е. q
— наибольшее из чисел 
и 
каждое из которых при условии (4.15)
строго меньше единицы.
2) Пусть t
— произвольное число, удовлетворяющее (4.15). Существует
начальное приближение 
при котором оценку (4.16) улучшить
нельзя, так как соотношение (4.16) превращается в точное равенство.
3) Если условие (4.15) не выполняется, то
существует при
котором последовательность не сходится с ростом p к
решению x.
4) Значение 
при котором q, задаваемое
формулой (4.17), принимает наименьшее значение* 
есть
В этом случае q принимает наименьшее значение
где 
— число обусловленности
оператора A.**
Замечание 1. Во многих случаях (например, при приближенной замене некоторых эллиптических краевых задач разностными) оператор A оказывается положительно определенным и самосопряженным в смысле некоторого естественного скалярного умножения. Однако обычно не удается точно указать его наибольшее и наименьшее собственные значения. Можно указать лишь общие оценки границ спектра, т. е. числа a и b такие, что выполняются неравенства
В этом случае также можно воспользоваться методом простых итераций. Сходимость окажется тем медленнее, чем хуже известны границы спектра a и b.
Замечание 2. Чем больше число обусловленности матрицы A, тем больше значение
и тем хуже
скорость сходимости. В некоторых случаях сходимость метода простых итераций для
плохо обусловленных систем уравнений можно существенно улучшить.
2.6.1 Переход к лучше обусловленной системе с помощью энергетически эквивалентного оператора
В случае плохо обусловленной системы Ax = f иногда удается перейти к равносильной системе с оператором, который имеет меньшее число обусловленности, а затем решить эту систему методом итераций.
Пусть 
— пока произвольный
оператор. Умножим обе части уравнения Ax = f на 
В результате получим
равносильное уравнение
Оператор C является
самосопряженным и положительно определенным в смысле скалярного произведения 
Имеет смысл выбирать оператор B лишь среди тех
операторов, для которых вычисление 
по заданному z существенно
проще, чем вычисление 
Если при этом удается выбрать B
так, чтобы он был «похож» на оператор A, то можно надеяться, что
оператор 
будет
«похож» на единичный, а его максимальное и минимальное собственные числа и
число обусловленности будут «ближе» к единице.
2.6.2 Масштабирование как средство улучшения числа обу-словленности
Прием масштабирования заключается
в следующем. Каждое из скалярных уравнений системы умножается на такой
множитель, чтобы максимальный коэффициент нового уравнения оказался равным
единице. От этой новой, масштабированной системы уравнений вида 
переходим к равносильной
системе с симметричной и положительно определенной матрицей путем умножения
обеих частей системы на 
2.7. Трехслойный метод Чебышева
Пусть 
а также известны числа a > 0
и b > 0, являющиеся границами спектра оператора A.
Зададим произвольное нулевое приближение и будем вычислять последующие приближения
по формулам:
где p = 1, 2, …; 
заданы как:
p = 1, 2, …
Можно показать, что погрешность приближения удовлетворяет оценке
p = 1, 2, …
Метод сходится тем быстрее, чем точнее определены границы спектра a и b.
Рассмотренный метод часто называют трехслойным методом
Чебышева в отличие от двухслойного метода Чебышева (см. ниже). Трехслойный метод
вычислительно устойчив, не уступает двухслойному методу по
скорости сходимости но, в отличие от последнего, не требует оптимизации порядка
выбора параметров 
Трехслойный
метод Чебышева уступает двухслойному методу по затратам памяти ЭВМ.
2.8. Метод с оптимальным набором параметров
Этот
метод является развитием метода простых итераций, когда параметр t зависит от номера итерации. Пусть 
Будем решать уравнение Ax = f
с помощью итерационного метода
p = 0, 1, 2, …, (4.18)
где — некоторое начальное приближение.
Зафиксируем
некоторое натуральное n. Поставим задачу выбрать такой набор
итерационных параметров 
…, 
при котором норма погрешности 
на n-й итерации
минимальна. Такими являются следующие параметры:
k = 1,
2, …, n, (4.19)
где
(4.20)
Здесь и — соответственно минимальное и максимальное
собственные значения.
Теорема 6. Если выбрать согласно (4.19) и
(4.20), то для погрешности 
справедлива оценка
где
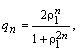
Итерационный метод (4.18)–(4.20) иногда называют двухслойным
итерационным методом Чебышева. Отметим, что связано с k-м
нулем многочленов Чебышева.
Как уже отмечалось выше, при проведении вычислений
с ограниченным числом значащих цифр двухслойный метод может оказаться
неустойчивым к росту ошибок округления. Для устойчивости метода необходимо
упорядочить набор параметров 
Этой проблемы можно избежать, применяя
трехслойный метод Чебышева, описанный выше. В настоящее время двухслойный метод
применяется редко.
2.9. Метод минимальных невязок
Пусть по-прежнему матрица Обозначим через
(4.21)
невязку,
получающуюся при подстановке некоторого значения в уравнение Ax = f.
Итерационный алгоритм запишем в виде
p = 0, 1, 2, …, (4.22)
где — некоторое начальное приближение.
Методом
минимальных невязок называется итерационный метод (4.22), в котором 
выбирается из условия
минимума 
при
заданной норме 
Минимум
нормы невязки достигается,
если
Метод минимальных невязок (4.22), (4.23) сходится с той же скоростью, что и метод простой итерации с оптимальным параметром.
Метод минимальных невязок по своей идее близок к методу сопряженных градиентов и отличается от последнего функционалом, который минимизируется на каждом шаге итераций.
2.10. Метод скорейшего спуска
Пусть матрица Рассмотрим итерационный алгоритм
(4.22) из предыдущего раздела:
p = 0, 1, 2, …
Здесь
— некоторое начальное
приближение.
Определим
вектор 
Введем
норму
В методе скорейшего спуска
находится из
условия минимума 
при
заданном векторе 
Оказывается,
что
Метод скорейшего спуска сходится с такой же скоростью, что и метод простой итерации с оптимальным параметром.
2.11. Библиографическая справка
Прикладная (машинная) линейная алгебра — обширная, бурно развивающаяся отрасль математики. Для знакомства с ней рекомендуем книгу [5], в которой существует также обзор работ по данной тематике. Полезно также ознакомиться с работами [17–19], где обсуждаются различные аспекты линейной алгебры.
Отдельной темой является работа с матрицами специального вида — так называемыми разреженными матрицами, см. книги [5, 20, 21] и библиографии в них.
3. Задание
1. Численно решите систему
уравнений Ax = f размером N ´ N методом простой
итерации. Матрица A является треугольной. По диагонали у матрицы A
расположены числа, принимающие значение r, за исключением элемента 
который равен единице.
На одной диагонали выше главной элементы матрицы принимают значение 
остальные элементы
равны нулю. Правую часть системы считать нулевой.
Попытайтесь применить метод простой итерации с параметром, равным 1, для значений N = 5, 10, 20 и r = 3/2.
Как видим, необходимые и достаточные условия сходимости метода простой итерации выполнены (теорема 3 из п. 4.5 — метод простой итерации). Тем не менее, результат может оказаться отличным от ожидаемого. Подумайте, как это можно объяснить.
2. Попытайтесь решить методом сопряженных градиентов систему линейных уравнений с матрицей A и правой частью
Объясните полученный результат.
При решении систем уравнений с плохо обусловленной матрицей иногда помогает введение масштабирования. Нетрудно догадаться, к какому эквивалентному виду надо привести систему уравнений в задаче 2, чтобы можно было с успехом применить метод сопряженных градиентов. Аналогичный переход помогает и при решении системы задачи 3.
3. Методом
простых итераций со значением итерационного параметра t = 0,3 и начальным приближением 
решите систему с нулевой правой
частью и с матрицей:
Определите оптимальное значение t и сравните требуемое для сходимости число итераций с предыдущим. Объясните результат.
4. Найдите решение системы
простым методом Гаусса и с выбором главного элемента. Вычисления вести с двумя знаками. Объясните результаты.
4. Контрольные вопросы
1. Выпишите расчетные формулы для метода Зейделя и метода верхней релаксации.
2. Покажите, что для самосопряженной матрицы A число обусловленности для спектральной нормы
где l — собственное значение матрицы A. Покажите, что в этом
случае 
3. Как изменится число обусловленности матрицы, если умножить ее на ненулевую константу? Покажите, что для произвольных невырожденных матриц A и B выполняется неравенство
4. Дана система
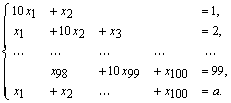
Предложите алгоритм, позволяющий экономно вычислять совокупность решений, отвечающих различным значениям a.
Указание. Алгоритм разобран в [17].
5. Рассмотрим матрицу A размером 30 ´ 30, где
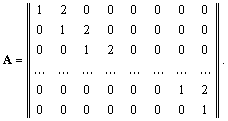
Оцените 
Наряду с A рассмотрите матрицу B, являющуюся возмущением A:
где матрица 
такая, что 
а остальные ее элементы равны
нулю. В этом случае 
Как
изменился определитель при переходе от матрицы A к матрице B?
5. Для системы
ответьте на следующие вопросы:
а) каково число обусловленности системы;
б) какова допустимая
относительная погрешность db при заданном фиксированном векторе 
при которой относительная
погрешность не превосходит 
в) каково наименьшее число m, при котором независимо от b и db выполняется оценка
верно для самосопряженной матрицы, если в 
выбрана норма вектора 